極小モデル、再帰的、機械学習: 少ないほど良い?

TRM とその効率とパフォーマンスへの影響に焦点を当て、機械学習における小さな再帰的モデルのトレンドを調査します。

The world of machine learning is constantly evolving, with researchers always seeking ways to improve performance and efficiency. Lately, there's been buzz around 'Tiny model, recursive, machine learning' approaches. Let's dive into what's shaking in this field.

機械学習の世界は常に進化しており、研究者はパフォーマンスと効率を向上させる方法を常に模索しています。最近、「極小モデル、再帰的、機械学習」のアプローチが話題になっています。この分野で何が起こっているのかを掘り下げてみましょう。

The Rise of Tiny Recursive Models

小さな再帰モデルの台頭

The recent work on TRM (Tiny Recursive Model) is questioning the necessity of complexity. TRM contains 5M-19M parameters, versus 27M in HRM. These models represent a fascinating shift towards simplicity and efficiency, challenging the conventional wisdom that bigger is always better.

TRM (Tiny Recursive Model) に関する最近の研究では、複雑さの必要性が疑問視されています。 TRM には 500 万～1900 万のパラメータが含まれていますが、HRM には 2700 万のパラメータが含まれています。これらのモデルは、シンプルさと効率性への魅力的な変化を表しており、大きいほど常に優れているという従来の常識に疑問を投げかけます。

TRM: A Closer Look

TRM: 詳細を見る

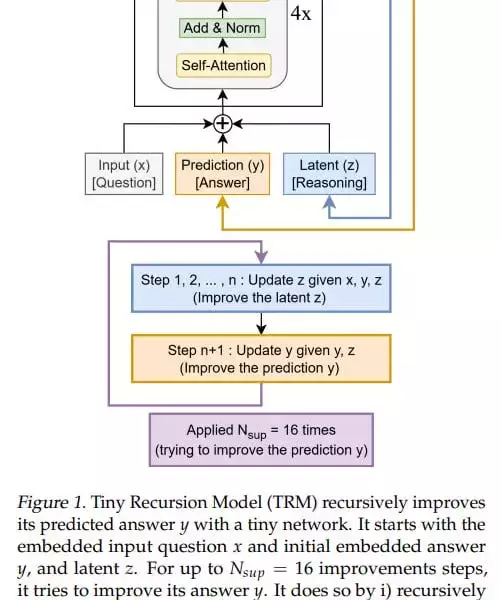
TRM simplifies the recursive process, designed with one small network, which is essentially a standard transformer block: [self-attention, norm, MLP, norm]. The model is designed so that there’s one small network, which is essentially a standard transformer block: [self-attention, norm, MLP, norm]. In the original idea, there were 4 such blocks (but after experiments they came to 2).

TRM は、基本的に標準の変換ブロックである 1 つの小さなネットワークで設計された再帰プロセスを簡素化します: [self-attention, Norm, MLP, Norm]。このモデルは、基本的に標準のトランスフォーマー ブロックである 1 つの小さなネットワークがあるように設計されています: [self-attention, Norm, MLP, Norm]。当初のアイデアでは、そのようなブロックは 4 つありました (ただし、実験の結果、2 つになりました)。

At the input, it has three elements: input (x), latent (z), and prediction (y); they’re all summed into one value. The basic iteration, analogous to the L module in HRM, generates a latent value (z, also denoted in the recursion formula as z_L) at the layer output, and the updated z goes back to the module input, where it now adds to input (x) not as zero. The output-prediction (y, also denoted in the formula as z_H) is also added, but since it hasn’t been updated, it doesn’t change anything.

入力には、入力 (x)、潜在 (z)、予測 (y) の 3 つの要素があります。それらはすべて 1 つの値に合計されます。基本的な反復は、HRM の L モジュールに似ており、レイヤ出力で潜在値 (z、再帰式では z_L とも表される) を生成し、更新された z はモジュール入力に戻り、そこでゼロではなく入力 (x) に加算されます。出力予測 (y、式では z_H としても示されます) も追加されますが、更新されていないため、何も変わりません。

Key Insights and Performance

重要な洞察とパフォーマンス

TRM achieves higher numbers than HRM: 74.7%/87.4% (attention version/MLP version) versus 55% for Sudoku, 85.3% (attention version, MLP version gives 0) versus 74.5% for Maze, 44.6%/29.6% (attn/MLP) versus 40.3% for ARC-AGI-1 and 7.8%/2.4% (attn/MLP) versus 5.0% for ARC-AGI-2. The experiments don’t look very expensive; runtime from <24 hours to about three days maximum on 4*H100 according to the repo.

TRM は HRM よりも高い数値を達成しています: 74.7%/87.4% (注意バージョン/MLP バージョン) 対 Sudoku の 55%、85.3% (注意バージョン、MLP バージョンは 0) 対 Maze の 74.5%、44.6%/29.6% (attn/MLP) 対 ARC-AGI-1 の 40.3% 7.8%/2.4% (attn/MLP) 対 ARC-AGI-2 では 5.0%。実験はそれほど高価ではないようです。リポジトリによると、4*H100 での実行時間は 24 時間未満から最大約 3 日間です。

My Two Cents

私の 2 セント

While the theoretical underpinnings of why these recursions work so well might not be fully understood yet, the empirical results are hard to ignore. TRM's architectural inventiveness, as opposed to eternal model scaling, is a breath of fresh air. It would be interesting how it would be with dataset scaling.

これらの再帰がなぜこれほどうまく機能するのかという理論的基礎はまだ完全には理解されていないかもしれませんが、経験的な結果は無視することができません。 TRM のアーキテクチャ上の独創性は、永遠のモデル スケーリングとは対照的に、新鮮な空気の息吹です。データセットのスケーリングがどうなるかは興味深いでしょう。

Looking Ahead

将来を見据えて

The journey of 'Tiny model, recursive, machine learning' is just beginning. There's a lot more to explore. So, let's keep an eye on these tiny titans and see where they take us next. Good recursions to everyone!

「極小モデル、再帰的、機械学習」の旅はまだ始まったばかりです。探索すべきことはまだたくさんあります。それでは、これらの小さな巨人たちに注目して、彼らが次に私たちをどこへ連れて行ってくれるのか見てみましょう。皆さんも良い再帰を！